Cascade Inference: Memory Bandwidth Efficient Shared Prefix Batch Decoding
Many LLM inference tasks involves multiple independent text generation from a shared prefix (prompt), e.g. Self-Consistency, Tree of Thoughts and Skeleton-of-thought. Serving LLMs with common prefix could be memory and time-consuming, especially when common prefix is long and the number of requests is large: a possible use case is long document QA (Figure 1), multiple users interacts with ChatBot with the same document as prompt. While vLLM alleviate the memory issue by only storing one copy of the common prefix. However, it still suffers from the low-efficiency because the default PageAttention implementation do not optimize KV-Cache access to the shared prompt.
In this blog post, we introduce Cascade Inference, which simply decouples attention of shared prefix and unique suffixes, and enables storing shared KV-Cache in GPU shared memory (SMEM for short) for fast access in multiple requests. We show that Cascade Inference can greatly accelerate shared-prefix batch decoding operator, with up to 31x speedup compared to the baseline vLLM PageAttention implementation and 26x speedup compared to FlashInfer batch decoding operator without cascading on a H100 SXM 80GB. The kernels have been supported in FlashInfer as PyTorch and C++ APIs.
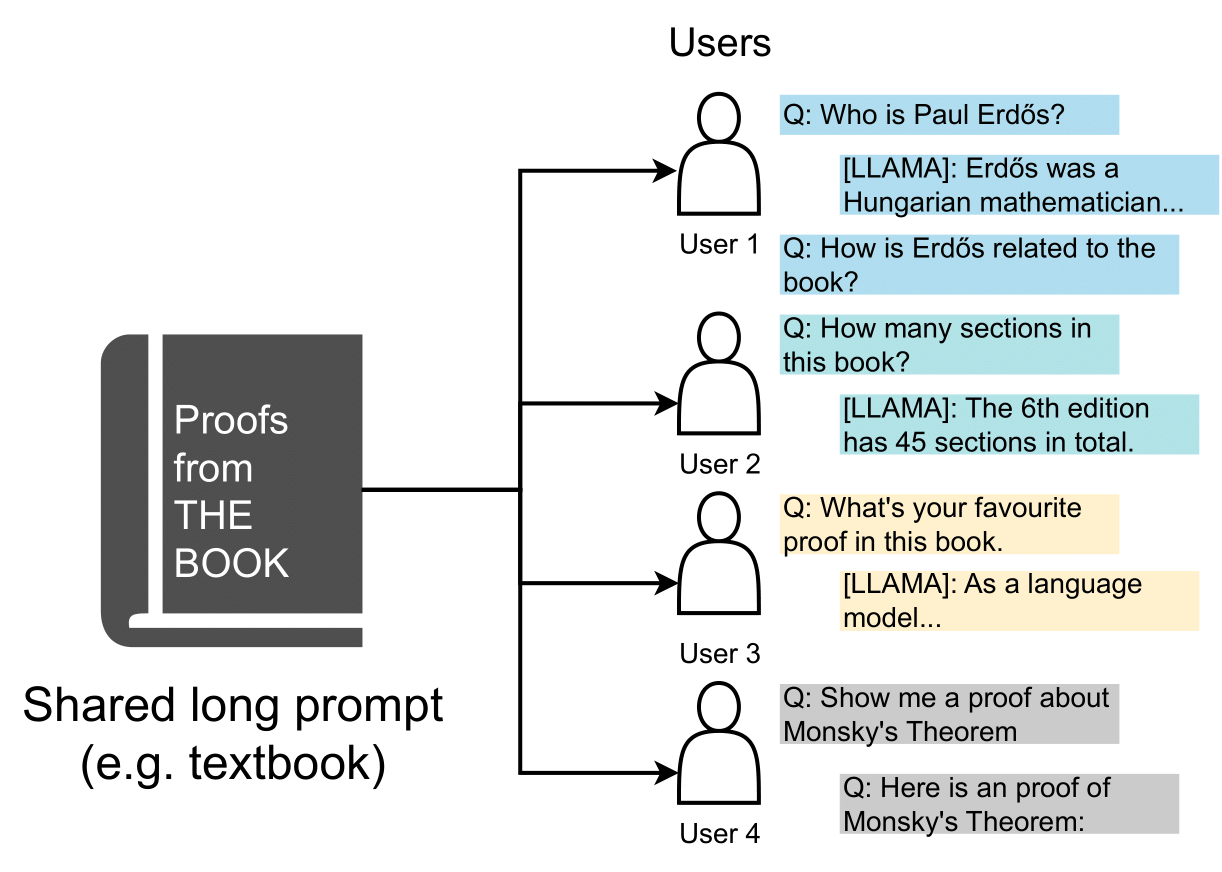
Figure 1. An example of serving Document QA for multiple users, all of the requests share the same book as prompt.
Background
GPU’s memory hierarchy is composed of global memory, L2 Cache, SMEM/L1 Cache and registers. While global memory and L2 Cache is shared across all streaming multiprocessors (SMs), SMEM/L1 Cache and registers are private to each SM. The throughput of accessing global memory and L2 Cache is much lower than that of accessing SMEM/L1 Cache and registers. Therefore, it is important to minimize the access to global memory and L2 Cache to achieve high throughput.
In CUDA programs, independent tasks are dispatched to different thread blocks 1, and each thread block is executed by one SM. For pre-Hopper architectures 2, each thread block can only access its local SMEM and registers.
Difference between Multi-Query and Single-Query CUDA Kernels
In multi-query attention (used in prefill/append) kernels, multiple queries access the same region of KV-cache. The usual implementation of multi-query attention kernel process multiple queries in a single thread block and loads KV-Cache to shared memory and computes the attention between multiple queries and the KV-Cache in parallel. This approach is bandwidth-efficient and can maximize TFLOPs/s by utilizing Tensor Cores, but not applicable if the KV-Cache for different queries are different.
The single-query attention kernel (used in decode), on the other hand, assumes that each query has its own KV-Cache, and batching cannot increase the operational intensity of this operator. In this case, there will be no benefit of processing multiple queries in a same thread block because the opportunity of reusing KV-Cache is limited. Most implementations of decode attention kernel process one query in a single thread block, to guarantee parallelism so that all SMs are fully utilized. However, this approach is not memory bandwidth efficient because each thread block needs to load the KV-Cache from global memory (or L2 cache, if the cache line has been hit before).
Divide and Conquer
Neither multi-query attention nor single-query attention kernel is a good fit for shared-prefix batch decoding. However, multi-query attention is perfect for attention between queries and shared prefix, while single-query attention can deal with the attention between queries and unique suffixes. Can we combine the advantages of both approaches?
Recursive Attention
The answer is “yes” if we can find a way to “merge” the attention of the same queries with shared prefix and unique suffixes. Fortunately, FlashAttention has shown it’s possible to combine local softmax/attention results by not only storing the local attention result, but also the normalization scales and renormalizing local attention results on the fly. Here we formulate the idea in concise notations:
Suppose $s_i$ is the pre-softmax attention score between query and the key at index $i$:
\[s_i = \mathbf{q}\mathbf{k}^T_i,\]we can generalize the definition from single index to an index set:
\[s(I) = \log\left(\sum_{i\in I} \exp(s_i) \right),\]let’s also generalize the value vector $\mathbf{v}$ from index to index sets (Note that the generalization of both $s$ and $\mathbf{v}$ are self-consistent: when $I$ equals $\{i\}$, we have $s(I) = s_i$ and $\mathbf{v}(I) = \mathbf{v}_i$):
\[\mathbf{v}(I) = \sum_{i\in I}\textrm{softmax}(s_i) \mathbf{v}_i = \frac{\sum_{i\in I}\exp\left(s_i\right)\mathbf{v}_i}{\exp(s(I))},\]the $\textrm{softmax}$ function is restricted to the index set $I$. Note that $\mathbf{v}(\{1,2,\cdots, n\})$ is the self-attention output of the entire sequence. The attention state between a query with KV of an index set $I$ can be defined as a tuple $\begin{bmatrix}\mathbf{v}(I) \\ s(I)\end{bmatrix}$, then we can define a binary merge operator $\oplus$ to combine two states as (in practice we will minus $s$ with maximum value to guarantee numerical stability and here we omit the trick for simplicity):
\[\begin{bmatrix}\mathbf{v}(I\cup J)\\s(I\cup J)\end{bmatrix}=\begin{bmatrix}\mathbf{v}(I)\\s(I)\end{bmatrix}\oplus\begin{bmatrix}\mathbf{v}(J)\\s(J)\end{bmatrix}=\begin{bmatrix} \frac{\mathbf{v}(I)\exp(s(I)) + \mathbf{v}(J)\exp(s(J))}{\exp(s(I)) + \exp(s(J))} \\ \log(\exp(s(I)) + \exp(s(J))) \end{bmatrix},\]the merge operator can be generalized to any number of attention state inputs:
\[\begin{bmatrix}\mathbf{v}(\bigcup_{i=1}^{n}I_i) \\ s(\bigcup_{i=1}^{n}I_i) \end{bmatrix} = \bigoplus_{i=1}^{n}\begin{bmatrix}\mathbf{v}(I_i) \\ s(I_i)\end{bmatrix} = \begin{bmatrix} \sum_{i=1}^{n} \textrm{softmax}(s(I_i))\mathbf{v}(I_i) \\ \log(\sum_{i=1}^{n} \exp (s(I_i))) \end{bmatrix}\]The above n-ary merge operator is consistent with the binary merge operator, and we can prove the operator is communicative and associative. There are different ways to get the attention state of the entire sequence by merging the attention states of index subsets, and the final outcome is mathematically equivalent:
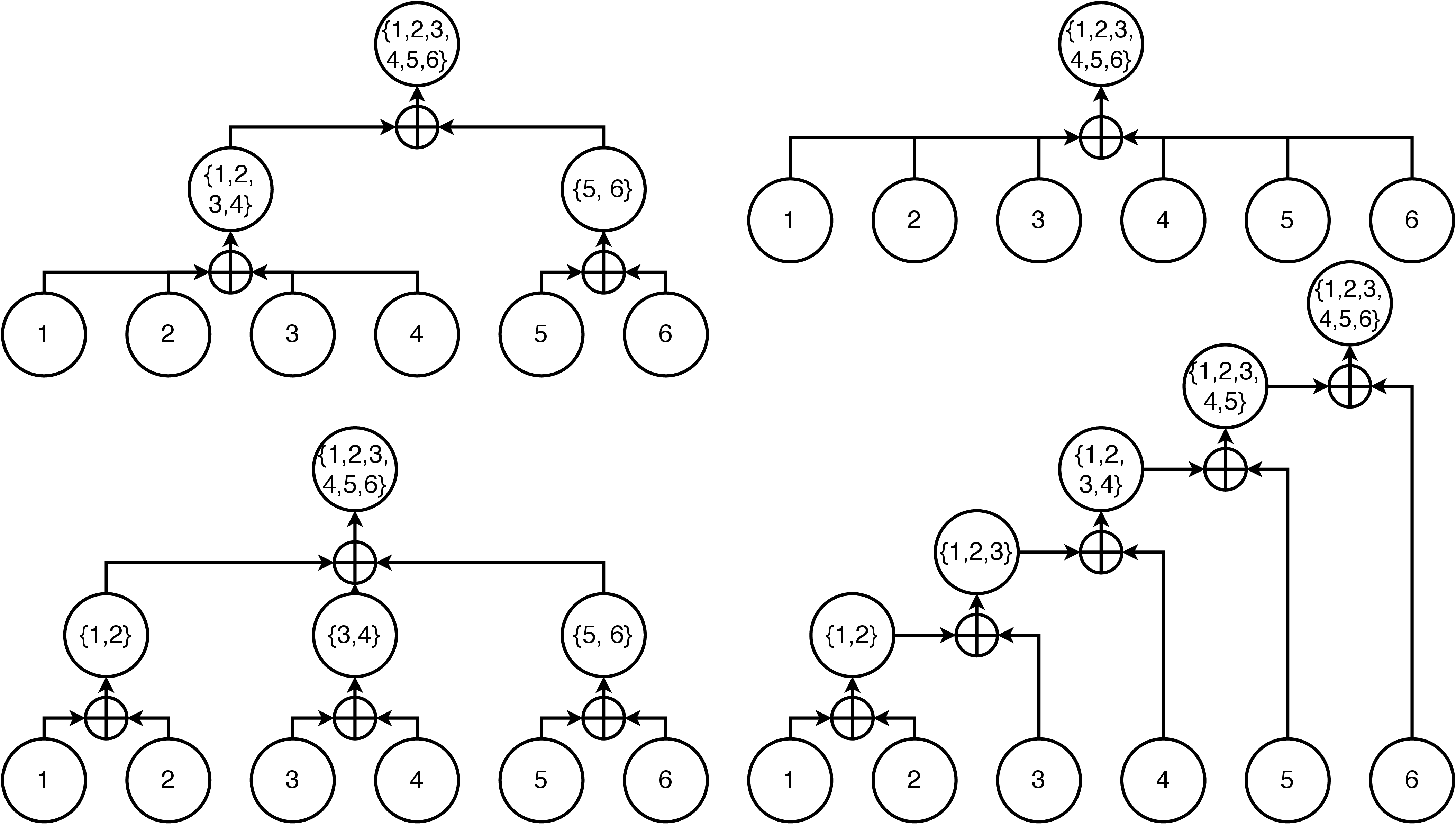
Figure 2. Different order to merge attention states are mathematically equivalent.
Recursive Attention allow us to decompose attention computation into multiple stages, different stages can be dispatched to different compute units/devices. The KV sequence partitioning trick in FlashInfer and Flash-Decoding uses the same idea to merge partial attention states from different thread blocks.
Cascade Inference: The Algorithm
With the merge operator, we can dispatch attention on different KV subsets to different kernel implementations. For shared-prefix batch decoding attention, we propose the following Divide-and-Conquer algorithm:
- Use multi-query (prefill/append) attention kernel to compute the attention state between queries and KV-Cache of shared prefix.
- Use batch decode attention kernel to compute the attention state between queries and KV-Cache of unique suffixes.
- Use merge operator to combine two attention states to get the final attention output.
The overall workflow is explained on the left side of Figure 3, different color of rectangles are processed in different thread blocks in GPU. Note that for multi-query attention kernels, we access KV-Cache through SMEM or registers and for decode kernels we can only access KV-Cache through L2 Cache or Global Memory. Cascade Inference allow us to maximize memory reuse for common prefix, thus making the attention computation much more memory efficient.
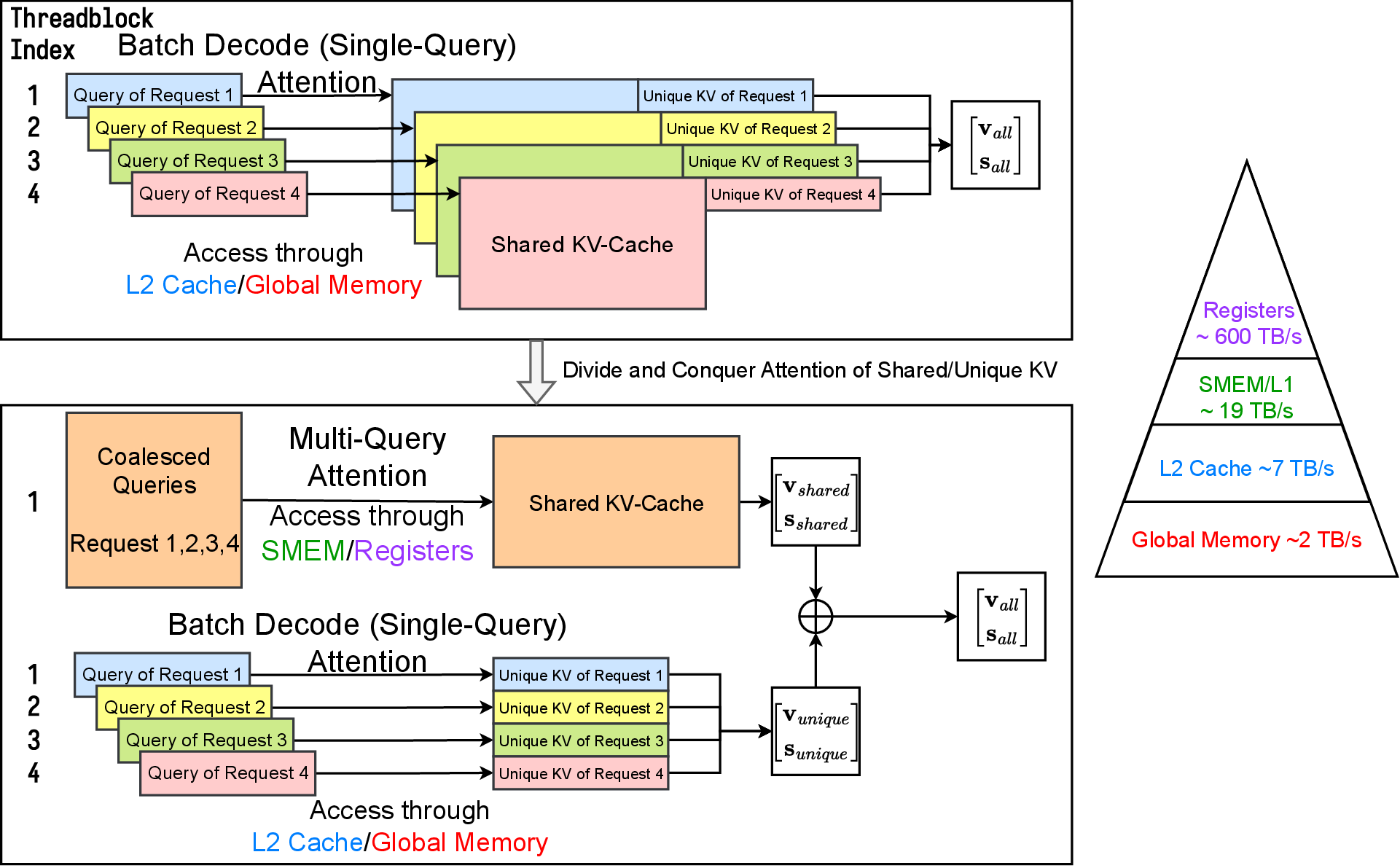
Figure 3. Workflow of Cascade Inference, throughput values adapted from blog: TPU vs GPU vs Cerebras vs Graphcore: A Fair Comparison between ML Hardware
We call the divide-and-conquer approach for shared-prefix attention the “Cascade Inference”.
Evaluations
We evaluate Cascade Inference on H100 SXM 80GB and A100 PCIE 80GB GPUs. The input shape are adapted from LLaMA2-7B (32 heads, 128 dimension per head). We varies three parameters: number of requests (batch size), shared prefix length and unique suffix length per request. The baseline implementations is PageAttention kernel implemented in vLLM 0.2.6, we also show the performance of FlashInfer batch decoding operator without cascading. The page size (or block size, equivalently) is fixed to 16 for all implementations (FlashInfer w/ and w/o cascading, vLLM PageAttention).
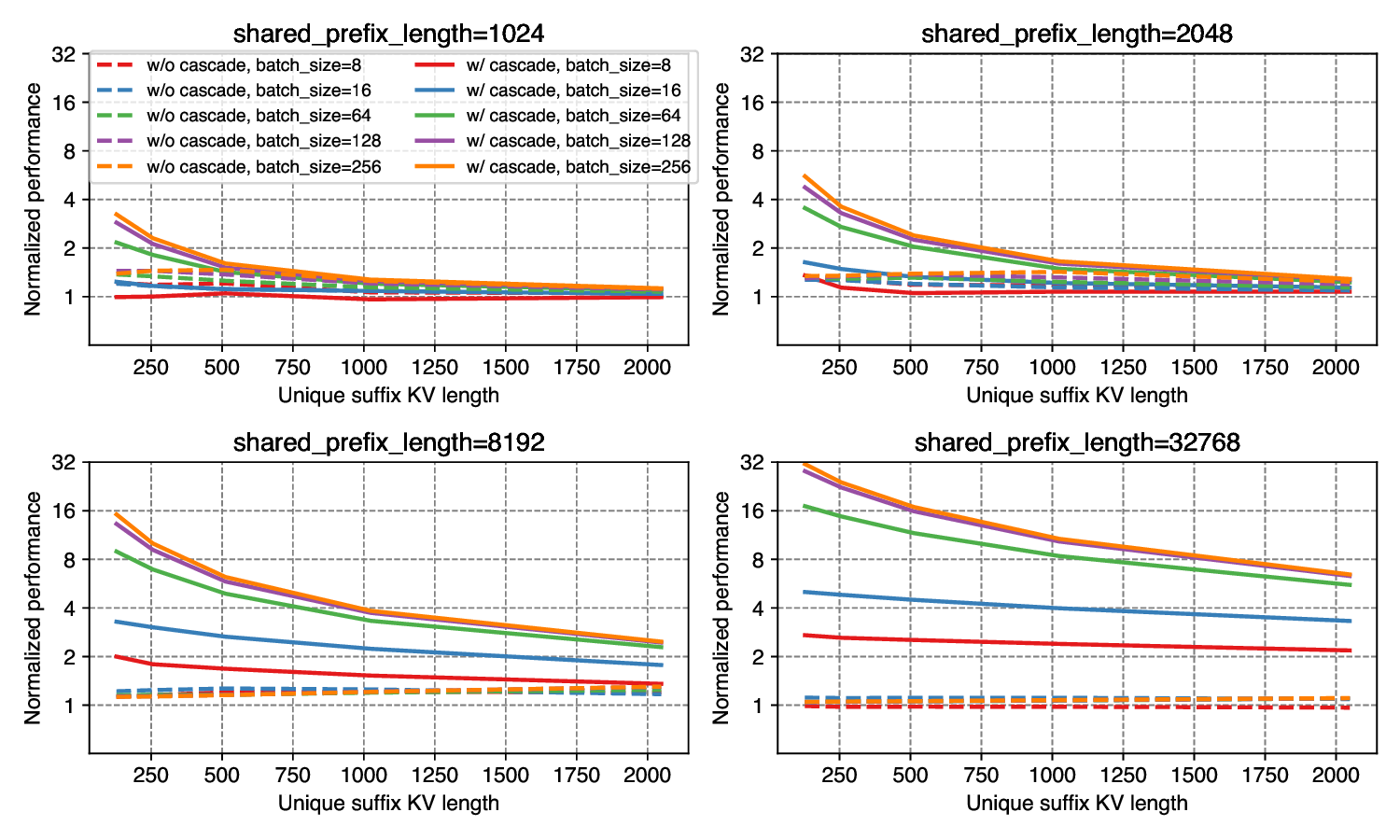
Figure 4. Speedup over vLLM PageAttention on H100 SXM 80GB
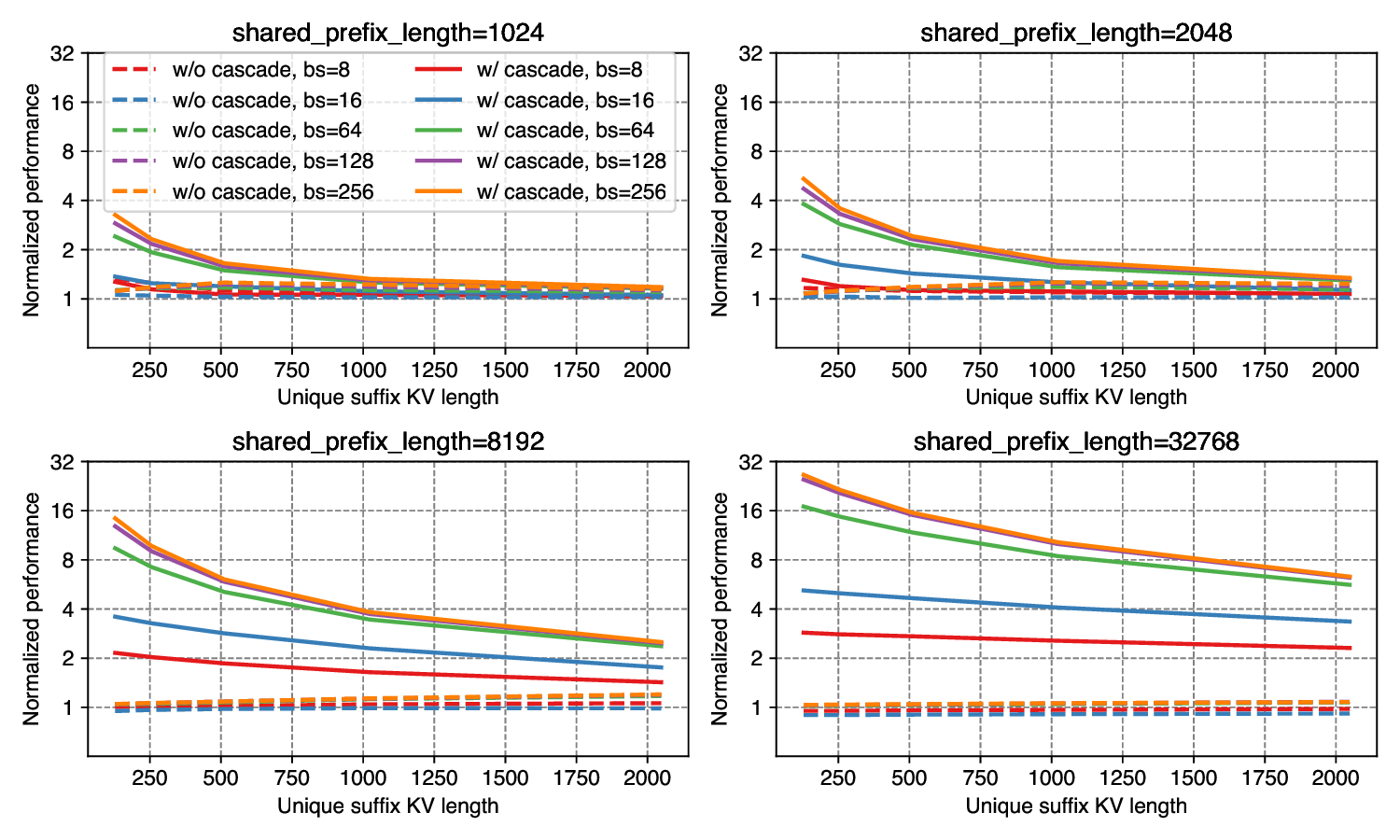
Figure 5. Speedup over vLLM PageAttention on A100 PCIe 80GB
Figure 4 and 5 show the normalized performance on FlashInfer kernels in cascading and non-cascading setting over vLLM implementation. FlashInfer kernels in both settings outperforms vLLM kernels, and cascading kernels significant speedup over non-Cascade Inference kernels in most cases. The benefit of cascade inference increases as shared prefix length and batch size grows (where the prefill kernel dominates execution time) and decreases as we increase unique suffix length (where the batch decode kernel dominates execution time). For very long shared prompt (32768), the decode kernel can get up to 31x speedup on H100 SXM 80GB with large batch size(≥128) and short unique kv-length (≤256).
Remarks and Future Work
The idea of Cascade Inference can be generalized to multiple levels (we only show two levels in this blog post) and multiple shared prefixes, the multi-level, multi shared-prefix Cascade Inference has been integrated to MLC-Serving: the universal serving framework based on MLC-LLM, we will show the end-to-end speedup in future blog posts.
Recently, SGLang (a domain-specific language for programming LLMs) proposes RadixAttention, where the KV-Cache is organized as a radix tree structure and the attention can be further accelerated with multiple-level Cascade Inference. We are collaborating with SGLang team to get this feature landed.
Citation
@misc{cascade-inference,
title = {Cascade Inference: Memory Bandwidth Efficient Shared Prefix Batch Decoding},
url = {https://flashinfer.ai/2024/02/02/cascade-inference.html},
author = {Ye, Zihao and Lai, Ruihang and Lu, Bo-Ru and Lin, Chien-Yu and Zheng, Size and Chen, Lequn and Chen, Tianqi and Ceze, Luis},
month = {February},
year = {2024}
}
Footnotes & References
-
thread block: the programming abstraction that represents a group of cooperative threads, one SM can execute multiple thread blocks and one thread block cannot span multiple SMs. ↩
-
Hopper architecture introduces a new abstraction called Thread Block Clusters which enables a thread block to access shared memory of other thread blocks within the same SM. Hopper also supports direct SM-to-SM communication without accessing global memory (a.k.a. Distributed Shared Memory), which can greatly accelerate cross-SM communication. However, these features are not available in pre-Hopper architectures such as A100 GPUs. ↩

Comments